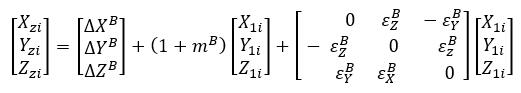坐标转换公式

坐标转换是空间实体的位置描述，是从一种坐标系统变换到另一种坐标系统的过程。通过建立两个坐标系统之间一一对应关系来实现。

（一）空间直角坐标与大地坐标间的转换

将同一坐标参照系下的大地坐标（B,L,H）转换为空间直角坐标（X,Y,Z）的公式为：

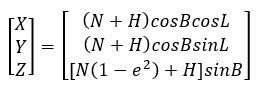
式中，N为卯酉圈的半径；e为参考椭球的第一偏心率。

空间直角坐标（X,Y,Z）转换为大地坐标（B,L,H）的公式为：

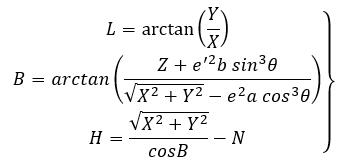
式中，e’为参考椭球的第二偏心率；，a为参考椭球的长半轴，b为参考椭球的短半轴。

（二）不同大地坐标系的三维转换

三维转换模型常用的有布尔莎模型（B模型）和莫洛坚斯基模型（M模型）等，布尔莎模型与莫洛坚斯模型的转换结果是等价的。布尔莎模型在全球或较大范围的基准转换时较为常用，布尔莎模型（B模型）如下。

设任意点O₁和O₂为原点的两坐标系中坐标分别为（X_1i，Y_1i，Z_1i）和（X_zi，Y_zi，Z_zi），布尔莎模型为：

式中，∆X^B 、∆Y^B 、∆Z^B为平移参数；为旋转参数；m^B为尺度变化参数。

注：三维坐标转换需要计算七个转换参数，至少需要三个公共点。